Volume Of Spherical Cap Calculator

You must select any one of these geometric shape and provide the required input fields. Hit on the volume button to see the exact results easily & quickly. In addition to the instant output, you can also find the formulas and step by step procedure to solve the volume.

Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere. N geometry, a spherical cap, spherical dome, or spherical segment of one base is a portion of a sphere cut off by a plane.

Volume is the quantification of the three-dimensional space a substance occupies. The SI unit for volume is the cubic meter, or m3. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces.

Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary.

Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes. A spherical cap or a spherical dome is a portion of a sphere or ball cut by a plane. It is also a spherical segment of a base, that is to say delimited by a single plane.

This function calculates the volume and surface area of a spherical cap. A spherical cap or spherical dome is a portion of a sphere cut off by a plane. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you.

It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. Online calculator to calculate the volume of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere and spherical cap.

You can figure the volume and surface area of a spherical cap if know its height and either the radius of its base or the radius of the larger sphere. The calculator below will compute the surface area and volume if you input the height H, and either the base radius A or sphere radius R. You can also apply the formulas described below. A spherical segment or a spherical layer is a three-dimensional geometrical object defined by cutting a sphere with a pair of two parallel planes.

The top and bottom planes, where intersecting the sphere, create two circles with radii b and a respectively, which serve as top and bottom bases of the segment. The height of the segment is the distance between the bases. The surface of the spherical segment is called spherical zone .

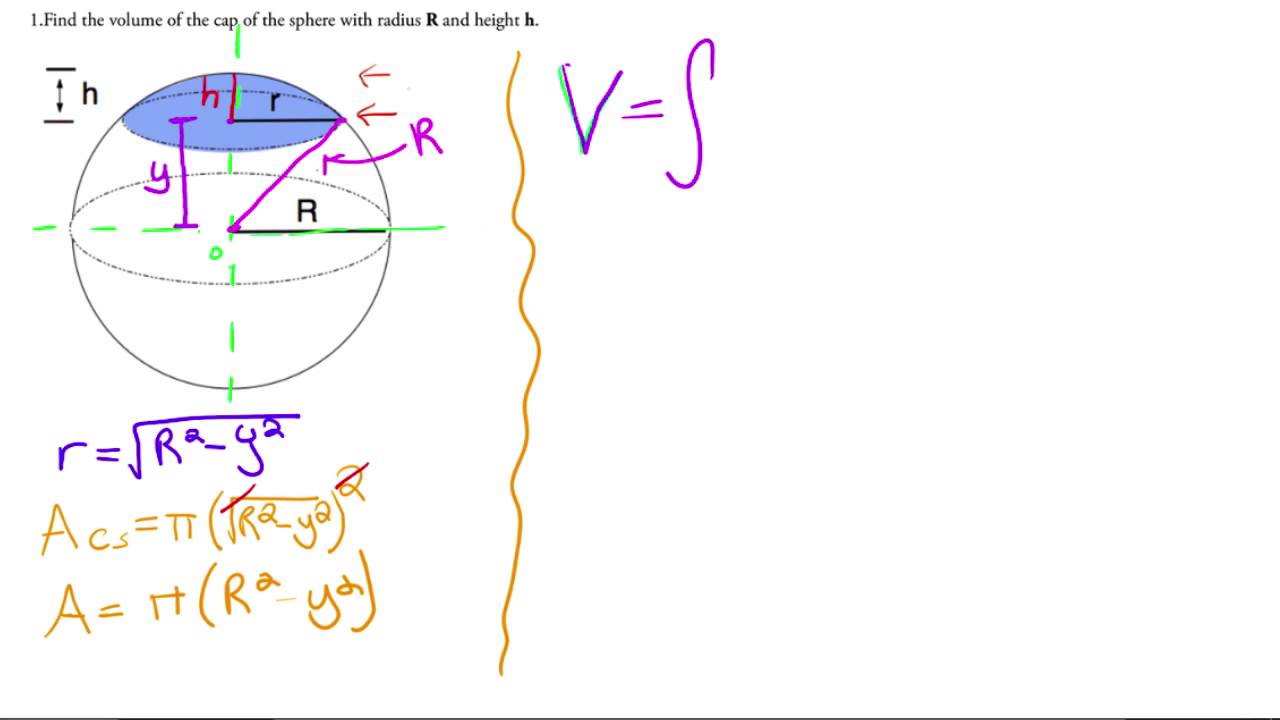
A spherical cap is a portion of a sphere cut off by a plane. The radius of the sphere is called r, the radius of the base of the cap called a, and the height of the cap called h. Almost all of the formulas for calculating the volume of a spherical cap use the radius of the sphere in the calculation. What if you don't know the radius of the sphere?

You would need to construct two separated planes tangent to the surface of the sphere and run a perpendicular from each plane into the sphere. The center of the sphere would be where the two perpendiculars cross. From that you could calculate the radius of the sphere. A spherical cap segment is the solid defined by cutting a sphere with a pair of parallel planes . It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum . This spherical cap volume calculator helps you find the volume of spherical caps.

If you ever wondered how to find the volume of a spherical cap, this calculator is here to help you. In this article, you can also find the formulas for obtaining spherical cap volume. We will also explain how to calculate the volume of spherical cap with an example.

Volume Of Cap Of Sphere Calculator Two online calculators to calculate the volume, surface area and height of a sphrical cup are presented. The calculators also computes the ratios of the volumes and ares of the cap and the sphere from which the cap is cut. A spherical cap is the region of a sphere which lies above a given plane. If the planepasses through the center of the sphere, the cap is a called a hemisphere, and if the cap is cut by a second plane, the spherical frustum is called a spherical segment.

However, Harris and Stocker use the term "spherical segment" as a synonym for what is here called a spherical cap and "zone" for spherical segment. Since the cylinder/cone and hemisphere have the same height, by Cavalieri's Principle the volumes of the two are equal. The cylinder volume is πR3, the cone is a third that, so the hemisphere volume is 23πR3. Thus the sphere of radius R has volume 43πR3. Online calculator which calculates the volume, lateral and total surface area of a spherical cap from the height, radius or circumference of a plane.

Determine the radius of the base of the cap. The spherical cap volume appears, as well as the radius of the sphere. They are equal to 287 cu in and 4.2 in for our example.

To calculate the volume of the full sphere, use the basic calculator. The spherical cap is the portion of a sphere that lies above a plane of the sphere. If the base area, height and the sphere radius is known then the volume can be found out of the particular portion. Spherical dome is the term used synonymously to the spherical cap. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere.

In geometry, a spherical dome also called spherical cap is a portion of a sphere cut off by a plane. To calculate Spherical cap height of Spherical Sector given volume and sphere radius, you need Volume Polyhedron & Radius 1 . With our tool, you need to enter the respective value for Volume Polyhedron & Radius 1 and hit the calculate button.

You can also select the units for Input and the Output as well. A spherical segment is the solid defined by cutting a sphere with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum. Cutting the sphere will create two regions. Both new parts of a sphere will be called spherical caps.

Basically, what you did is divide a circle using a plane and spherical caps are formed by a plane that is cutting a circle into two parts. There is no specific point where the plane can cut, it can cut in any direction but two new formed parts will be called spherical caps. Therefore, in simple words, a spherical cap is each of the parts of the sphere determined by a secant plane.

A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere.

A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent. All dome structures described by this calculator are a segment or "cap" of a sphere as defined by the dome's diameter and height.

The radius of curvature is the calculated radius of the whole sphere of which the dome is a portion. The overall diameter of the structure. The calculator applies the diameter to the floor, stem wall, and base of the spherical dome. 1 - Enter the radius \( R \) of the sphere from which the spherical cap is cut and the height \( h \) as positive real numbers, with \( R \ge h \) and press "calculate". Given radius of sphere, calculate the volume and surface area of sphere. A spherical lune is a part of a spherical wedge.

Basically, a spherical lune is the curvature part of the boundary of a spherical wedge. Take a look at the below picture. The red marks on the edge of the sphere entrap a space. That space is called a spherical lune. In simple words, a spherical lune is an area that is entrapped by two half circles that meet each other at the diameter.

Volume is the quantity of a three dimensional space enclosed by a closed surface. The space that a substance or shape occupies is also called the volume. The SI unit of volume is cubic meter. The part of a sphere cut off by a plane is called the spherical crown. The circle cut off is called the bottom of the spherical crown.

The section perpendicular to the diameter of the section is called the height of the crown. The spherical crown can also be regarded as a curved surface formed by the rotation of an arc around the diameter passing through one of its ends. A level input measures a slice of the structure. For example, it can calculate the area of a second floor, show headroom around the dome perimeter, or calculate the volume and surface area of a portion of the dome. A spherical cap is the region of a sphere that lies above a given plane.

If the plane passes through the center of the sphere, the cap is called a hemisphere. This distance r is the radius of the sphere, and the given point is the center of the sphere. To find the volume, you can use the below formula.

All you need is the value of segment radius, radius of the sphere, and the height between the segment and the plane. If you have all the information available, just use the below formula to find the volume of a spherical segment. The volume of a spherical cap means the total space occupied by the spherical cap. To find the volume, you can use the below formula, nothing additional information is required for the calculation of the volume. The spherical wedge is the part of a sphere between two planes that intersect at the diameter. Both planes are semidisk and wedge's base.

Below are the pictures of a sphere where the spherical wedge is indicated. Spherical cap 4 What is the surface area of a spherical cap, the base diameter 20 m, height 2.5 m? Spherical cap The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.

If the radius of the small circle is the same as that of the sphere, then the spherical cap is called a hemisphere. Enter the radius and height of a spherical cap into the calculator to determine both the volume and area of the cap. A spherical segment is the part of the sphere between two parallel cutting planes. The surface area of the spherical segment is called the zone. You can find the radius of the sphere with the help of the radius of the plane and the height between the plane and the sphere. Below is the formula to find the radius of the sphere using the spherical cap.

We have different ways to calculate the hemisphere volume based on the available parameters. Sometimes in the question you will be given the base radius while in some you will be given as the sphere radius. IT important to differentiate and use the respective formula to find the surface area. Spherical cap Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which the spherical cap was cut.